Kernel PCA with python(Radial Basis Function, RBF)
from scipy.spatial.distance import pdist, squareform
from numpy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
sq_dists=pdist(X, 'sqeuclidean')
mat_sq_dists=squareform(sq_dists)
K=exp(-gamma*mat_sq_dists)
N=K.shape[0]
one_n=np.ones((N,N))/N
K=K-one_n.dot(K)-K.dot(one_n)+one_n.dot(K).dot(one_n)
eigvals, eigvecs=eigh(K)
eigvals, eigvecs=eigvals[::-1], eigvecs[:,::-1]
X_pc=np.column_stack([eigvecs[:,i] for i in range(n_components)])
return X_pc
임의로 비선형데이터를 만들고 테스트 하기
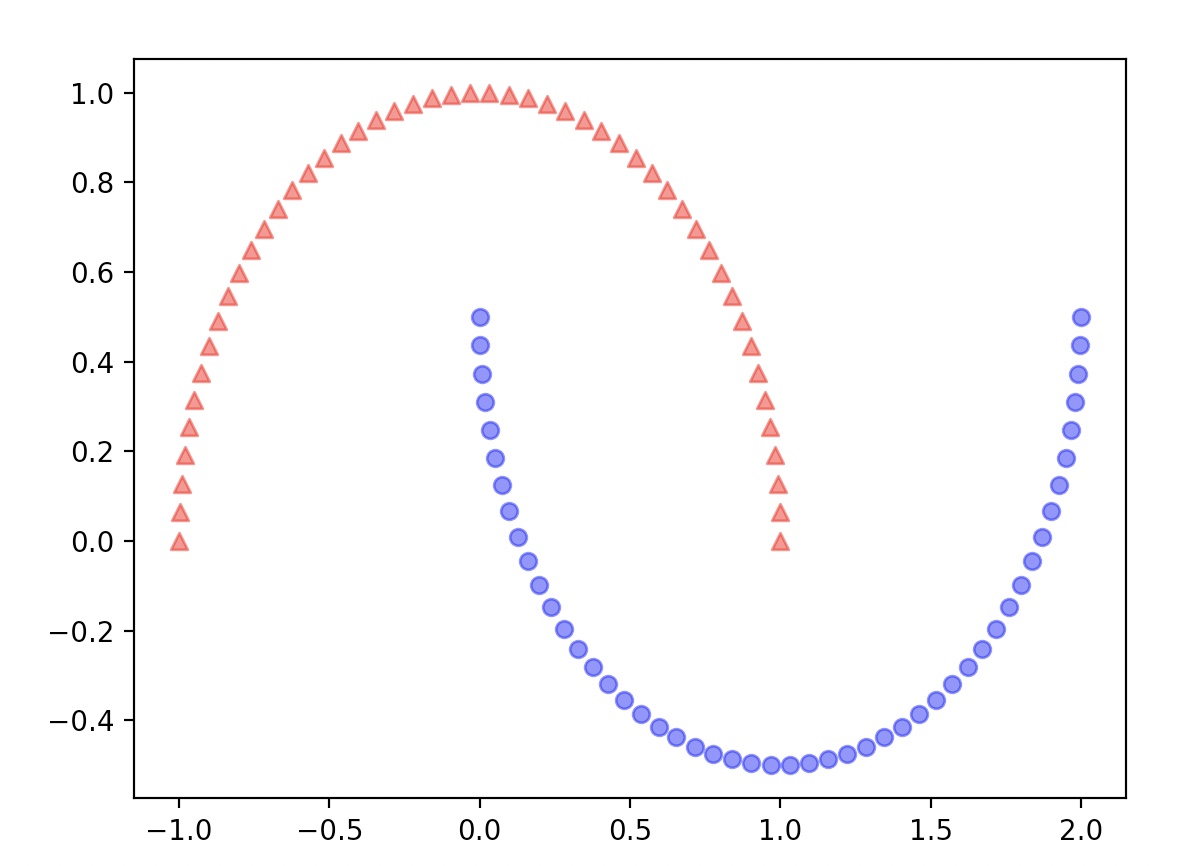
1. 반달 모양
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
X, y=make_moons(n_samples=100, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.show()
PCA
from sklearn.decomposition import PCA
scikit_pca=PCA(n_components=2)
X_spca=scikit_pca.fit_transform(X)
fig, ax=plt.subplots(nrows=1, ncols=2, figsize=(7,3))
ax[0].scatter(X_spca[y==0, 0],X_spca[y==0, 1], color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1], color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y==0, 0], np.zeros((50, 1))+0.02, color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((50, 1))-0.02, color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1,1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.show()

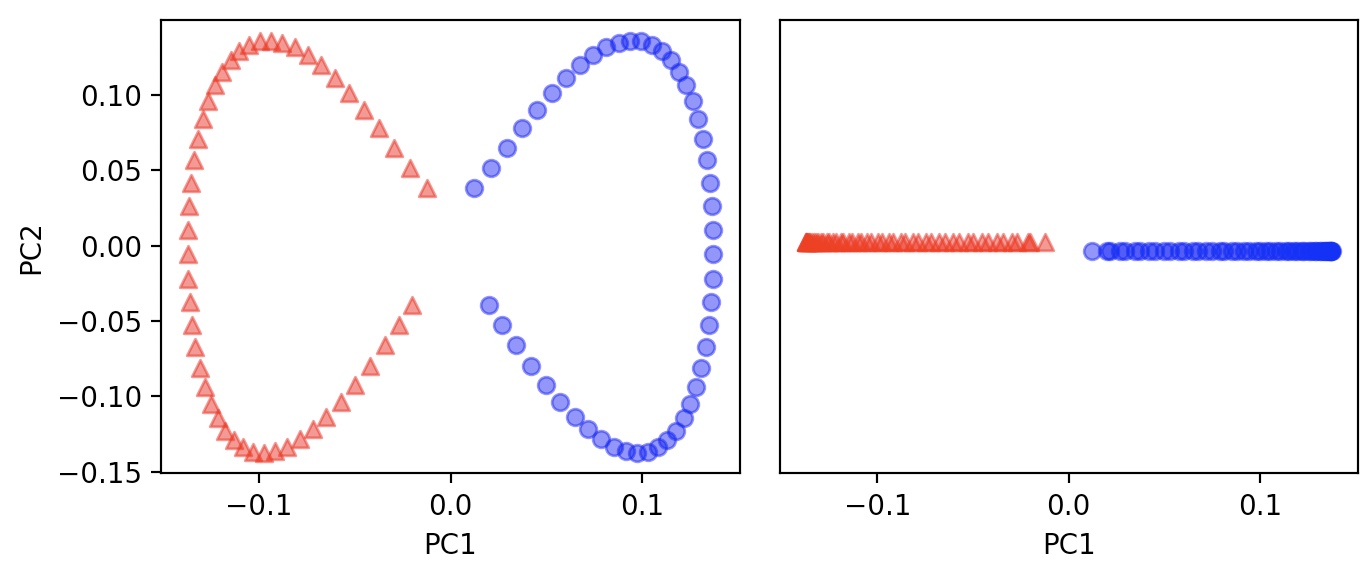
PCA를 통해서 비선형 데이터셋을 잘 구분하지 못한다.
ax[1]는 첫 번째 주성분만 그렸을 때 구분
ax[0]는 원래 반달 모양이 조금 변형되었고, 수직 축을 기준으로 반전되었다.
(판별하는데 선형 분류기에 도움이 되지는 않는다
PCA는 비지도 학습 방법이기 때문에 클래스 레이블 정보를 사용하지 않는다.
위 그래프에서 기호는 구분이 잘되는지 확인하기 위해서 사용한 것임-> 분류에 영향을 미치지 않음
RBF kernel PCA
X_kpca=rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax=plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1], color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1], color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((50, 1))+0.02, color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((50, 1))-0.02, color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()
여러가지 데이터셋에 잘 맞는 보편적인 gamma 파라미터 값은 없다.
주어진 문제에 적합한 gamma값을 찾으려면 실험을 통해서 찾아야 한다.
이 후 6장에서 파라미터 최적화 작업을 통해서 최적화 작업을 자동화 시킬 것임
2. 동심원 모양
from sklearn.datasets import make_circles
X, y=make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.tight_layout()
plt.show()

PCA
scikit_pca=PCA(n_components=2)
X_spca=scikit_pca.fit_transform(X)
fig, ax=plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1], color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1], color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y==0, 0], np.zeros((500, 1))+0.02, color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((500, 1))-0.02, color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylable('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()
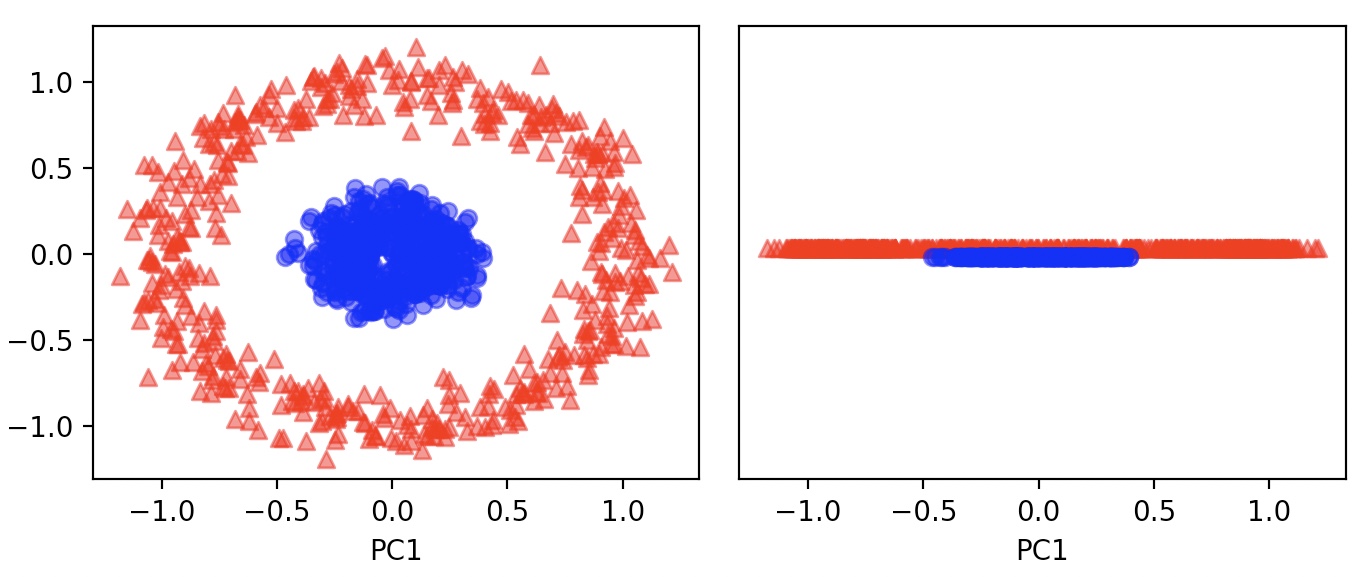
RBF kernel PCA
X_kpca=rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax=plt.subplots(nrows=1, ncols=2, figsize=(7,3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1], color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1], color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((500, 1))+0.02, color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((500, 1))-0.02, color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()

새로운 데이터 포인트 투영
일반적으로 변환해야 할 데이터셋이 하나 이상이다. (훈련 데이터셋+테스트 데이터셋…)
kernel PCA에서 샘플은 이미 주성분 축 v에 투영되어 있다.
따라서 새로운 샘플 x’를 주성분 축에 투영하려면 phi(x’).T.dot(v)를 계산하여야 한다.
커널트릭을 사용하면 명시적으로 투영 phi(x’).T.dot(v)를 계산할 필요는 없다.
기본 PCA와 달리 kernel PCA는 메모리 기반 방법이다.(새로운 샘플을 투영하기 위해서 매번 원본 훈련 데이터셋을 재사용)
훈련 데이터셋에 있는 i번 째 새로운 샘플과 새로운 샘플 x’ 사이 RBF 커널(유사도)를 계산하여야 한다.
머신러닝교과서with파이썬, 사이킷런, 텐서플로_개정3판pg.230
커널 행렬의 고윳값도 반환하도록 수정한
rbf_kernel_pca
from scipy.spatial.distance import pdist, squareform
from numpy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
sq_dists=pdist(X, 'sqeuclidean')
mat_sq_dists=squareform(sq_dists)
K=exp(-gamma*mat_sq_dists)
N=K.shape[0]
one_n=np.ones((N,N))/N
K=K-one_n.dot(K)-K.dot(one_n)+one_n.dot(K).dot(one_n)
eigvals, eigvecs=eigh(K)
eigvals, eigvecs=eigvals[::-1], eigvecs[:,::-1]
alphas=np.column_stack([eigvecs[:, i] for i in range(n_components)])
lambdas=[eigvals[i] for i in range(n_components)]
return alphas, lambdas
새로운 반달 데이터셋을 만들고 수정된 커널 PCA 구현을 사요해서 1차원 부분 공간에 투영
X, y=make_moons(n_samples=100, random_state=123)
alphas, lambdas=rbf_kernel_pca(X, gamma=15, n_components=1)
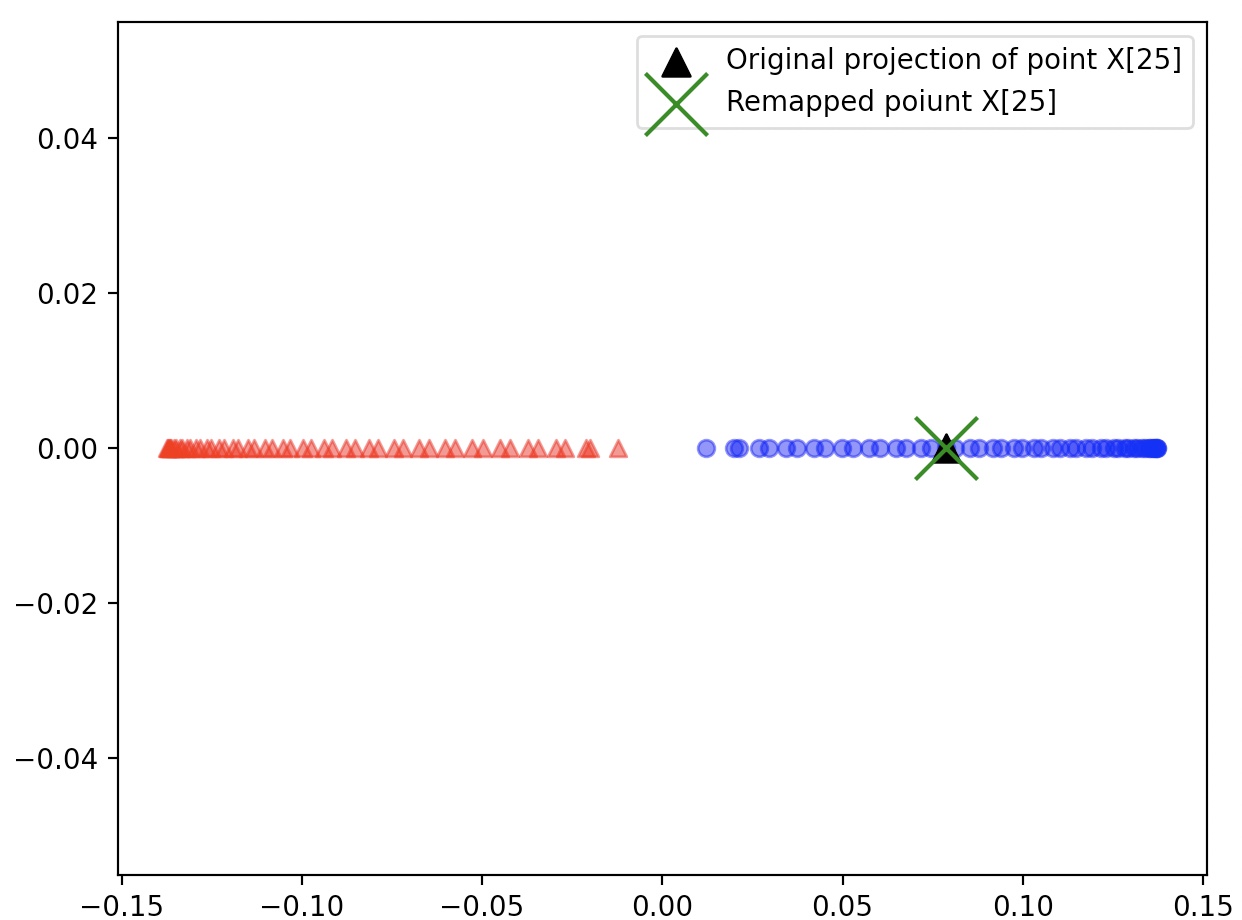
26번째 포인트가 새로운 데이터 포인트 x’라고 가정->이 포인트를 새로운 부분 공간으로 투영
x_new=X[25]
x_new
array([1.8713187 , 0.00928245])
x_proj=alphas[25]
x_proj
array([0.07877284])
원본 투영 재현
def project_x(x_new, X, gamma, alphas, lambdas):
pair_dist=np.array([np.sum((x_new-row)**2) for row in X])
k=np.exp(-gamma*pair_dist)
return k.dot(alphas/lambdas)
x_reproj=project_x(x_new, X, gamma=15, alphas=alphas, lambdas=lambdas)
x_reproj
array([0.07877284])
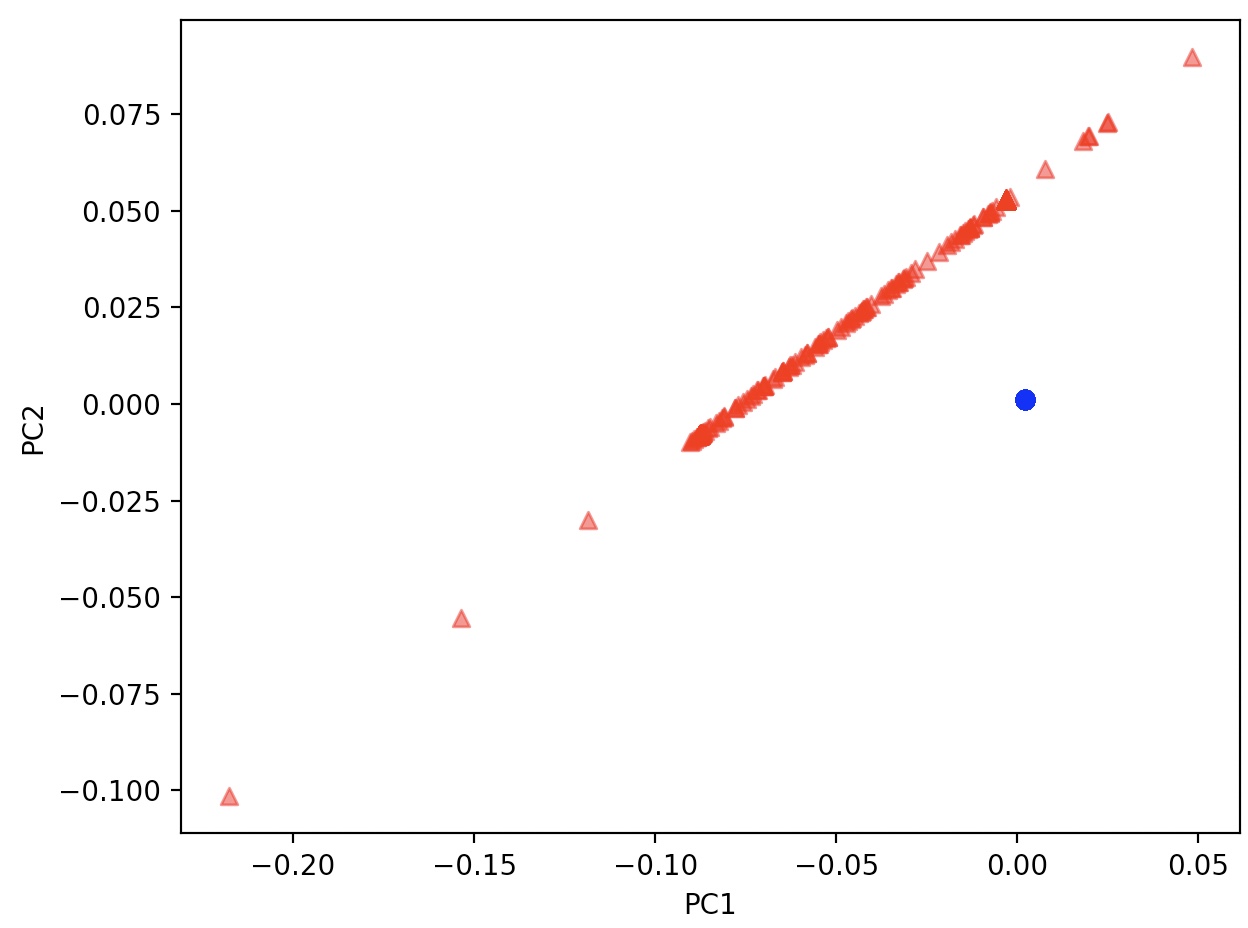
plt.scatter(alphas[y==0, 0], np.zeros((50)), color='red', marker='^', alpha=0.5)
plt.scatter(alphas[y==1, 0], np.zeros((50)), color='blue', marker='o', alpha=0.5)
plt.scatter(x_proj, 0, color='black', label='Original projection of point X[25]', marker='^', s=100)
plt.scatter(x_reproj, 0, color='green', label='Remapped point X[25]', marker='x', s=500)
plt.legend(scatterpoints=1)
plt.tight_layout()
plt.show()
scikit-learn PCA
from sklearn.decomposition import KernelPCA
X, y=make_moons(n_samples=100, random_state=123)
scikit_kpca=KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca=scikit_kpca.fit_transform(X)
plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
plt.show()
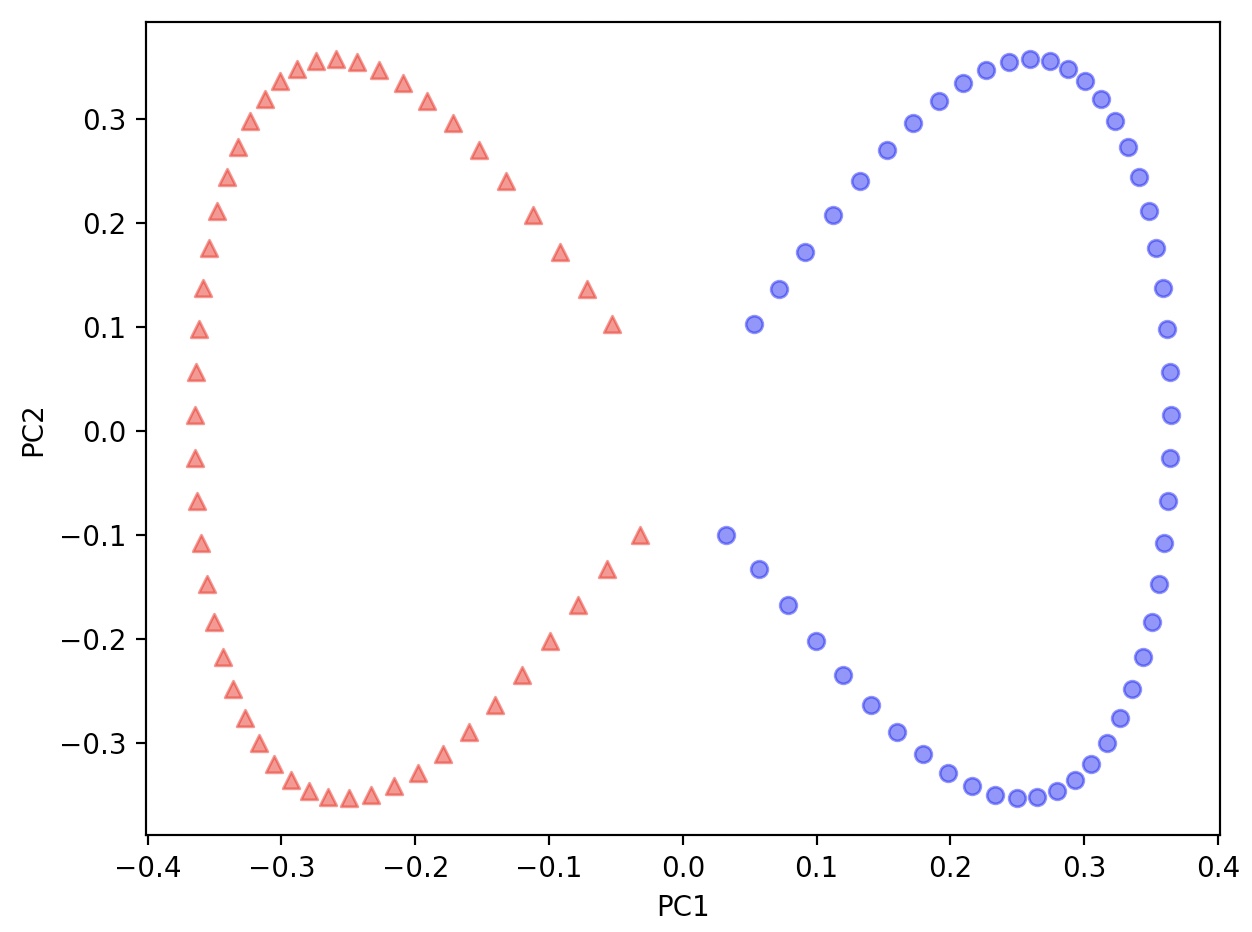
매드폴드 학습(manifold learning)
사이킷런 라이브러리가 제공하는 비선형 차원 축소를 위한 고급 기법
def plot_manifold(X, y):
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
plt.show()
Locally Linear Embedding, LLE
반달 모양 데이터셋을 지역선형 임베딩(Locally Linear Embedding, LLE)에 적용
LLE는 이웃한 샘플간의 거리를 유지하는 저차원 투영을 찾는다.
from sklearn.manifold import LocallyLinearEmbedding
lle=LocallyLinearEmbedding(n_components=2, random_state=1)
X_lle=lle.fit_transform(X)
plot_manifold(X_lle, y)

반달 모양은 유지되지 않았지만, 뚜렷하게 두 클래스가 구분되었다.
s-distributed Stochastic Neighbor Embedding ,t-SNE
t-SNE(t-distributed Stochastic Neighbor Embedding)은 데이터 포인트 간의 유사도를
결합 확률(joint probability)로 변환하고, 저차원과 고차원의 확률 사이에서 쿨백-라이블러(Kullback-Leibler)
발산을 최소화한다.
t-SNE는 특히 고차원 데이터셋을 시각화하는 성능이 뛰어나다.
from sklearn.manifold import TSNE
tsne=TSNE(n_components=2, random_state=1)
X_tsne=tsne.fit_transform(X)
plot_manifold(X_tsne, y)
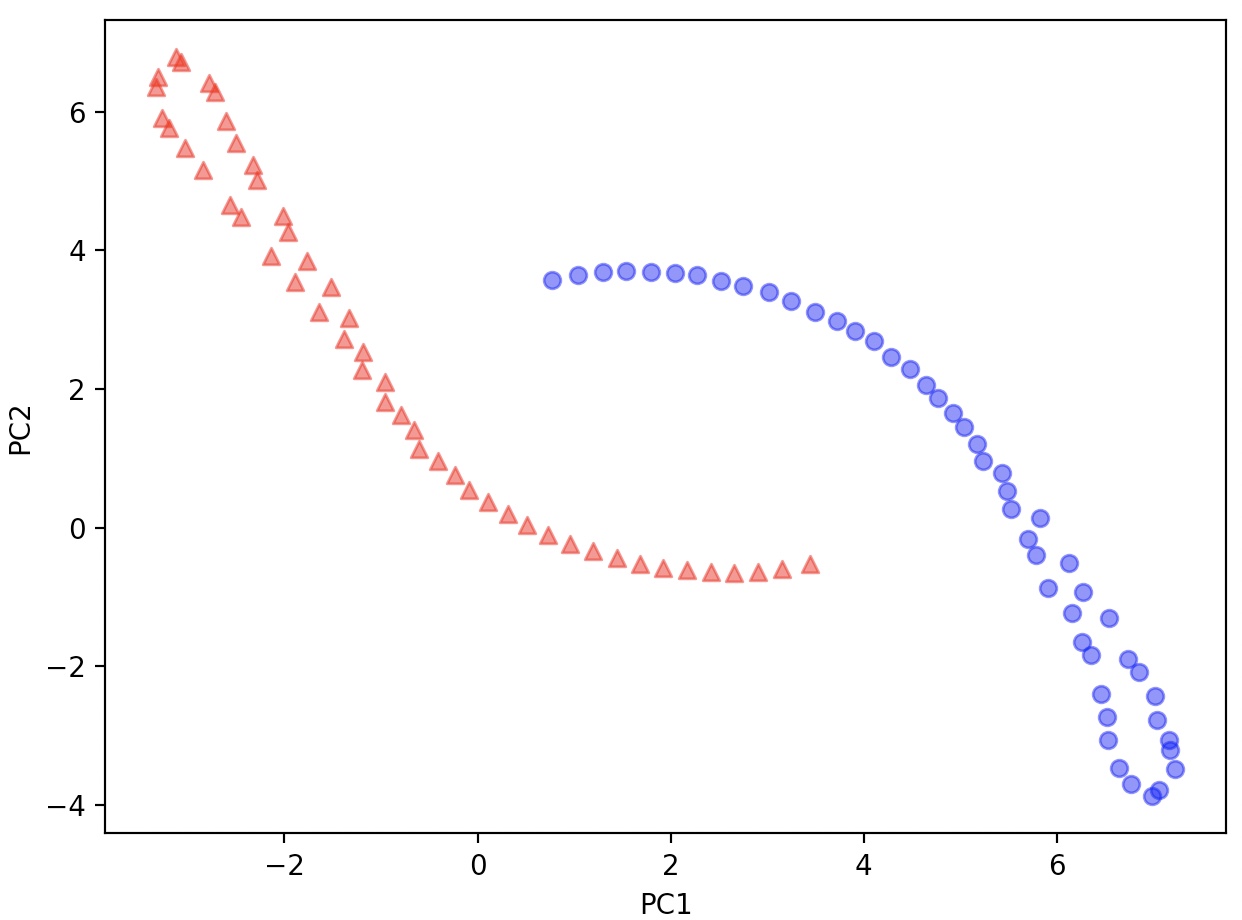
t-SNE는 두 클래스를 선형적으로 잘 분리하며, 원래 반달 모양도 어느 정도 유지하고 있다.
동심원 데이터셋에 적용(kernelPCA, LocallyLinearEmbedding, TSNE)
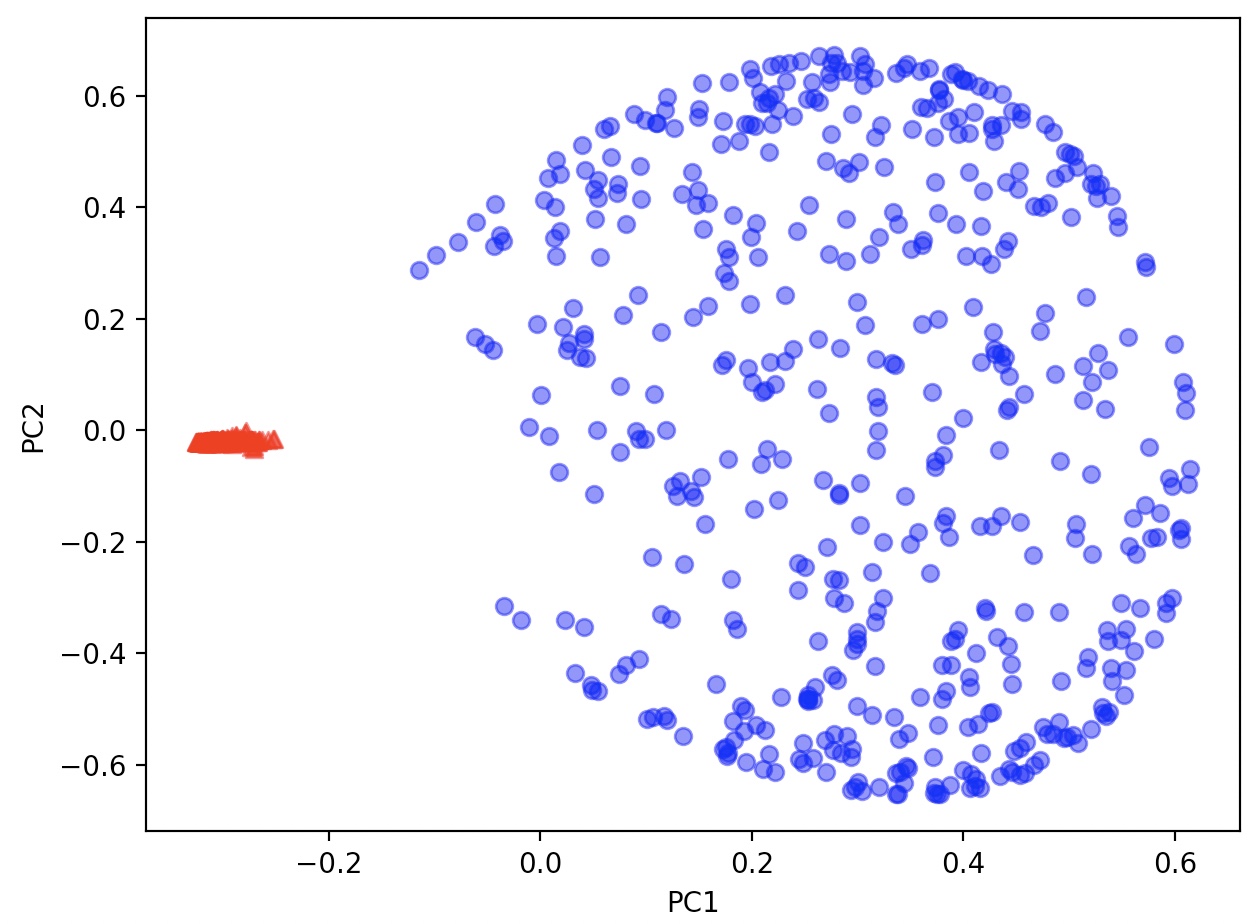
from sklearn.datasets import make_circles
X, y=make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
scikit_kpca=KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca=scikit_kpca.fit_transform(X)
plot_manifold(X_skernpca, y)
from sklearn.manifold import LocallyLinearEmbedding
lle=LocallyLinearEmbedding(n_components=2, random_state=1)
X_lle=lle.fit_transform(X)
plot_manifold(X_lle, y)
from sklearn.manifold import TSNE
tsne=TSNE(n_components=2, random_state=1)
X_tsne=tsne.fit_transform(X)
plot_manifold(X_tsne, y)
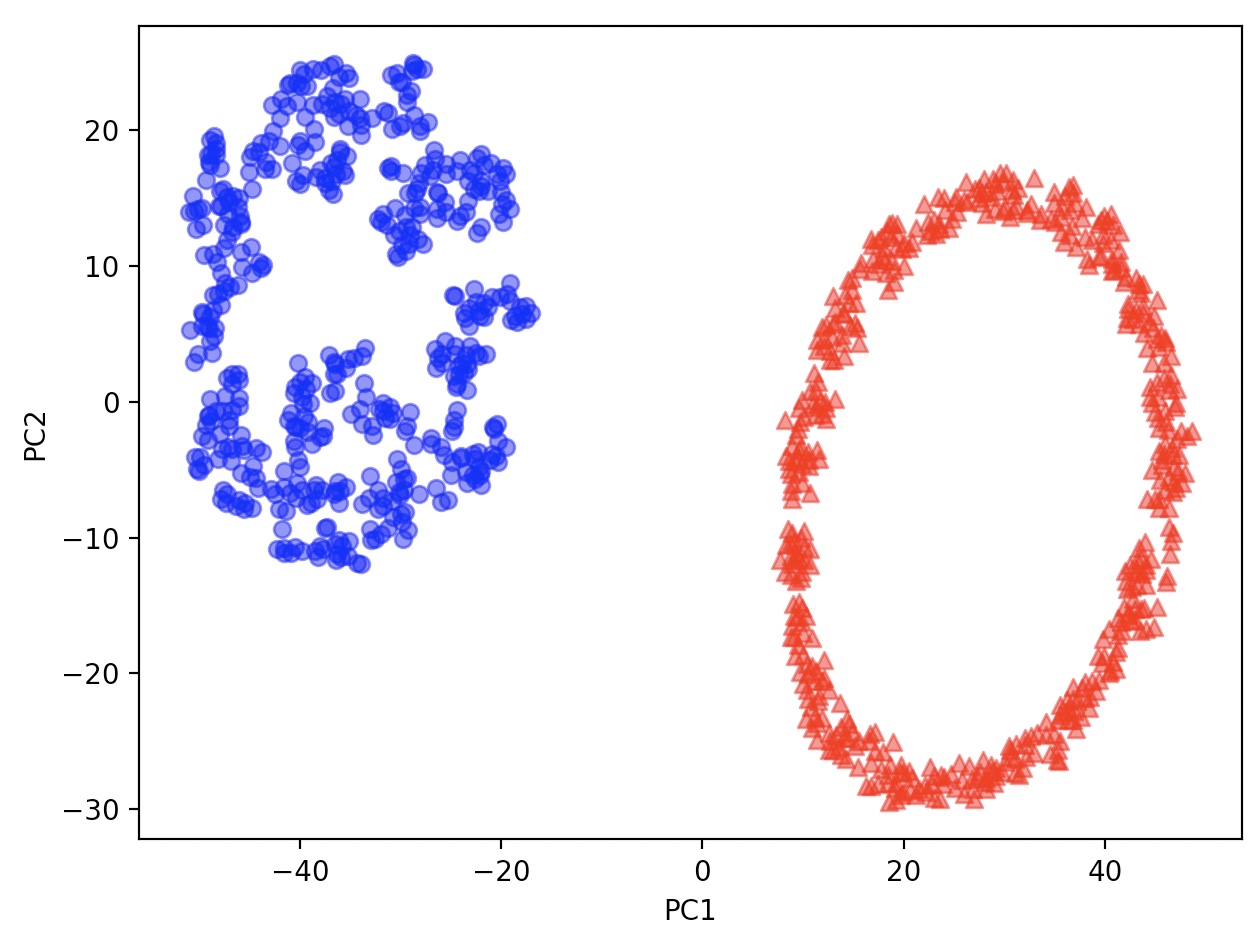
t-SNE를 사용하면 두 동심원을 완변하게 분리했을 뿐 아니라, 동심원의 모양도 거의 보존해 준다.